数组

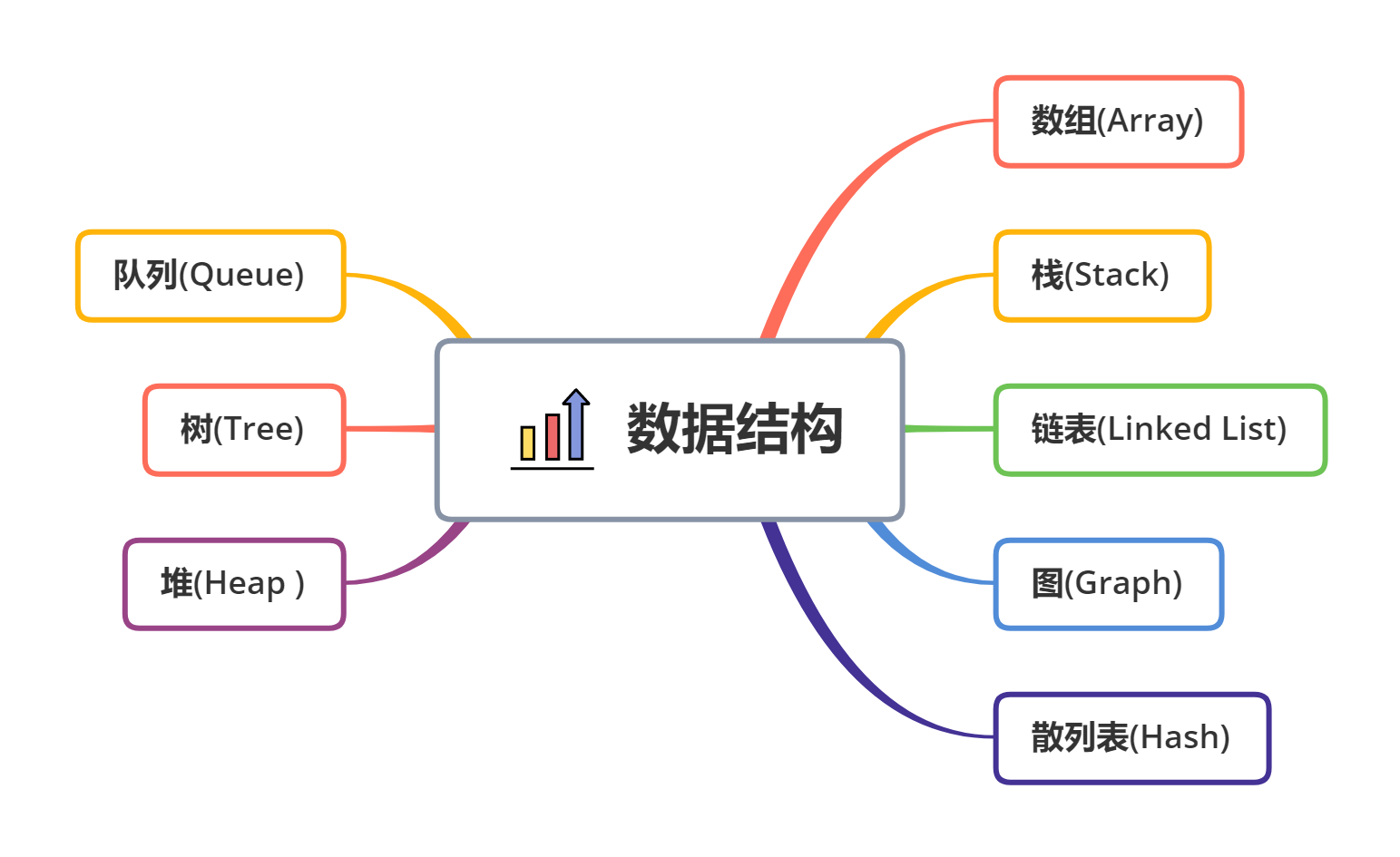
队列

队列是一种受限的序列，它只能够操作队尾和队首，并且只能在队尾添加元素，在队首删除元素。队列 (queue) 是一种特殊类型的抽象数据类型或集合，集合中的实体按顺序保存。

队列基本操作有两种：

向队列的后端位置添加实体，称为入队

从队列的前端位置移除实体，称为出队。

栈

栈也是一种受限的序列，它只能够操作栈顶，不管入栈还是出栈，都是在栈顶操作。栈 (stack) 是一种抽象数据类型，用作表示元素的集合，具有两种主要操作：

push, 添加元素到栈的顶端（末尾）

pop, 移除栈最顶端（末尾）的元素

此外，应有一个 peek 操作用于访问栈当前顶端（末尾）的元素。（只返回不弹出）

链表

散列表

堆

堆其实是一种优先级队列，插入、删除元素的时间复杂度为：O(log n)

堆的特点：

在一个 最小堆 (min heap) 中，如果 P 是 C 的一个父级节点，那么 P 的 key（或 value) 应小于或等于 C 的对应值。 正因为此，堆顶元素一定是最小的，我们会利用这个特点求最小值或者第 k 小的值。

在一个 最大堆 (max heap) 中，P 的 key（或 value) 大于或等于 C 的对应值。

树

二叉树

二叉树是节点度数不超过二的树，是树的一种特殊子集，二叉树（英语：Binary tree）是每个节点最多只有两个分支（即不存在分支度大于2的节点）的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序（普通树的节点无左、右次序之分），不能随意颠倒。

二叉树的第 i 层至多拥有 2^(i-1) 个节点；深度为 k 的二叉树至多总共有 2^k-1个节点

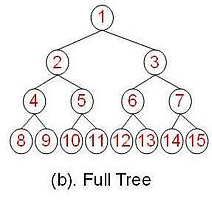
满二叉树

一棵深度为 k，且有 2^k-1 个节点的二叉树，称为满二叉树（Full Binary Tree）。这种树的特点是每一层上的节点数都是最大节点数。

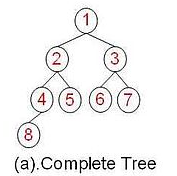
完全二叉树

在一颗二叉树中，若除最后一层外的其余层都是满的，并且最后一层要么是满的，要么在右边缺少连续若干节点，则此二叉树为完全二叉树（Complete Binary Tree）

二叉查找树

（英语：Binary Search Tree），也称为有序二叉树（ordered binary tree）或排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树：

1. 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
2. 若任意节点的右子树不空，则右子树上所有节点的值均大于或等于它的根节点的值；
3. 任意节点的左、右子树也分别为二叉查找树；

二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低，为 O(log n)

在二叉查找树 b 中查找 x 的过程为：

若 b 是空树，则搜索失败，否则：

若 x 等于 b 的根节点的数据域之值，则查找成功；否则：

若 x 小于 b 的根节点的数据域之值，则搜索左子树；否则：

查找右子树。

向一个二叉查找树 b 中插入一个节点 s 的算法，过程为：

若 b 是空树，则将 s 所指节点作为根节点插入，否则：

若 s->data 等于 b 的根节点的数据域之值，则返回，否则：

若 s->data 小于 b 的根节点的数据域之值，则把 s 所指节点插入到左子树中，否则：

把 s 所指节点插入到右子树中。（新插入节点总是叶子节点）

平衡树

是改进的二叉查找树，二叉查找树的查询复杂度取决于树的深度，当节点深度比较大时，查询均摊的复杂度会上升，为了实现更高效的查询，产生了平衡树。

在这里，平衡指所有叶子的深度趋于平衡，更广义的是指在树上所有可能查找的均摊复杂度偏低。几乎所有平衡树的操作都基于树旋转操作（也有部分基于重构，如替罪羊树），通过旋转操作可以使得树趋于平衡。二叉树旋转前后，中序遍历的结果不变。因此树的任何部分旋转，对整棵树的元素顺序没有影响

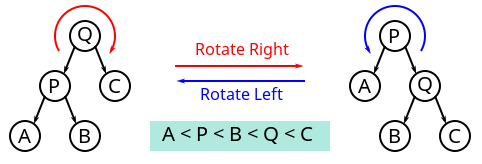
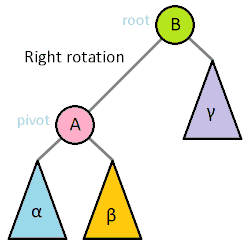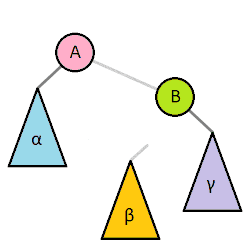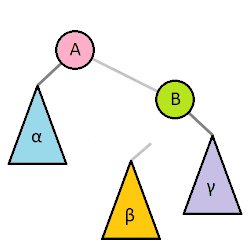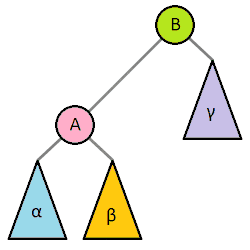
红黑树、AVL树、树堆、伸展树、加权平衡树、2-3树、AA树（红黑树的一种变种）都是平衡树

红黑树

（英语：Red–black tree）是一种自平衡二叉查找树，红黑树的结构复杂，但它的操作有着良好的最坏情况运行时间，并且在实践中高效：它可以在 O(log n) 时间内完成查找、插入和删除，这里的 n 是树中元素的数目

红黑树是每个节点都带有颜色属性的二叉查找树，颜色为红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求：

1. 节点是红色或黑色。
2. 根是黑色。
3. 所有叶子都是黑色（叶子是NIL节点）。
4. 每个红色节点必须有两个黑色的子节点。（从每个叶子到根的所有路径上不能有两个连续的红色节点。）
5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

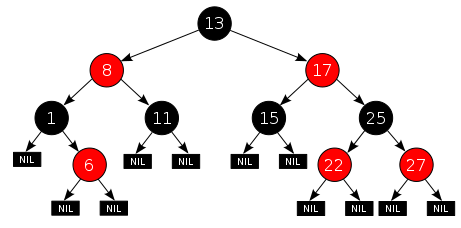
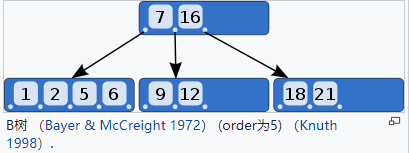
B树

（B-tree）是一种自平衡的树，一般化的二叉查找树，一个节点可以拥有2个以上的子节点（节点内的元素是有序的），能够保持数据有序。与自平衡二叉查找树不同，B树适用于读写相对大的数据块的存储系统，例如磁盘。B树减少定位记录时所经历的中间过程，从而加快存取速度。B树这种数据结构可以用来描述外部存储。这种数据结构常被应用在数据库和文件系统的实现上。

在B树中，内部（非叶子）节点可以拥有可变数量的子节点（数量范围预先定义好）。在一个2-3 B树（通常简称2-3树），每一个内部节点只能有2或3个子节点。下面B树内部有5个子节点。

B+ 树

通常用于数据库和操作系统的文件系统中。B+ 树的特点是能够保持数据稳定有序，其插入与修改拥有较稳定的对数时间复杂度。B+ 背后的想法是内部节点可以有在预定范围内的可变量目的子节点。因此，B+ 树不需要像其他自平衡二叉查找树那样经常的重新平衡。

在 B+ 树中的节点通常被表示为一组有序的元素和子指针。如果此 B+ 树的阶数是 m，则除了根之外的每个节点都包含最少 m/2 个元素最多 m-1 个元素，对于任意的结点有最多 m 个子指针。对于所有内部节点，子指针的数目总是比元素的数目多一个。所有叶子都在相同的高度上，叶结点本身按关键字大小从小到大链接。

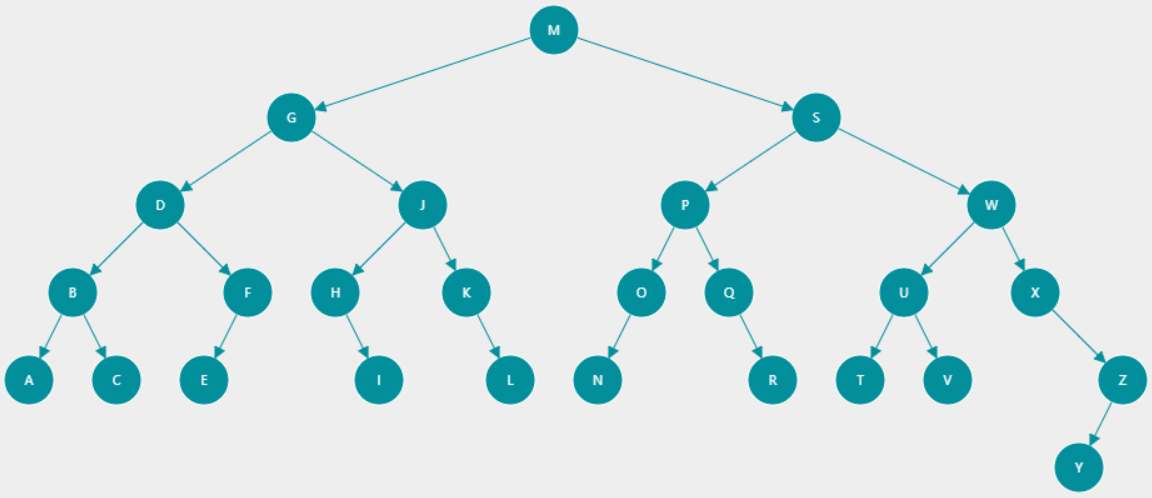
节点遍历

1. 深度优先遍历
   前序遍历的结果：M，G，D，B，A，C，F，E，J，H，I，K，L，S，P，O，N，Q，R，W，U，T，V，X，Z，Y
   后序遍历的结果：A，C，B，E，F，D，I，H，L，K，J，G，N，O，R，Q，P，T，V，U，Y，Z，X，W，S，M
   中序遍历的结果：A，B，C，D，E，F，G，H，I，J，K，L，M，N，O，P，Q，R，S，T，U，V，W，X，Y，Z

2. 广度优先遍历
   会先访问离根节点最近的节点。二叉树的广度优先遍历又称按层次遍历。算法借助队列实现。

3. Z 字形遍历
   从左到右，然后下一层从右到左，然后再变化方向，就是这样一层一层的遍历

4. 层次遍历
   给定一个二叉树 {3,9,20,#,#,15,7}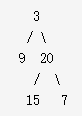

   

   返回的层次遍历的结果是：{3,20,9,15,7}

哈希

散列表（Hash table，也叫哈希表），是根据键 Key 而直接访问在内存储存位置的数据结构。也就是说，它通过计算一个关于键值的函数，将所需查询的数据映射到表中一个位置来访问记录，这加快了查找速度。这个映射函数称做散列函数，存放记录的数组称做散列表。

哈希冲突

由于通过哈希函数产生的哈希值是有限的，而数据可能比较多，导致经过哈希函数处理后仍然有不同的数据对应相同的值。这时候就产生了哈希冲突。

解决哈希冲突的四种方法

1. 开放地址方法

   • 线性探测：按顺序决定值时，如果某数据的值已经存在，则在原来值的基础上往后加一个单位，直至不发生哈希冲突。

   • 再平方探测：按顺序决定值时，如果某数据的值已经存在，则在原来值的基础上先加 1 的平方个单位。随之是 2 的平方，3 的平方等等。直至不发生哈希冲突。

   • 伪随机探测：按顺序决定值时，如果某数据已经存在，通过随机函数随机生成一个数，在原来值的基础上加上随机数，直至不发生哈希冲突。

2. 链式地址法（HashMap 的哈希冲突解决方法）

   对于相同的值，使用链表进行连接。使用数组存储每一个链表。

   • 优点：

   拉链法处理冲突简单，且无堆积现象，即非同义词决不会发生冲突，因此平均查找长度较短；由于拉链法中各链表上的结点空间是动态申请的，故它更适合于造表前无法确定表长的情况；

   在用拉链法构造的散列表中，删除结点的操作易于实现。只要简单地删去链表上相应的结点即可。

   • 缺点：

   指针占用较大空间时，会造成空间浪费，若空间用于增大散列表规模进而提高开放地址法的效率。

   1. 建立公共溢出区存储所有哈希冲突的数据。
   2. 再哈希法，对于冲突的哈希值再次进行哈希处理，直至没有哈希冲突。

一致性哈希

传统的哈希算法在分布式下指定节点为 node_number = hash(key) % N, 其中 N 为节点数。当某节点宕机或者新加节点时，所有映射关系都将出错需要重新做映射，为此提出一致性哈希。

一致性哈希算法通过一个叫作一致性哈希环的数据结构实现。这个环的起点是 0，终点是 2^32-1，并且起点与终点连接，故这个环的整数分布范围是 [0, 2^32-1]，如下图所示：

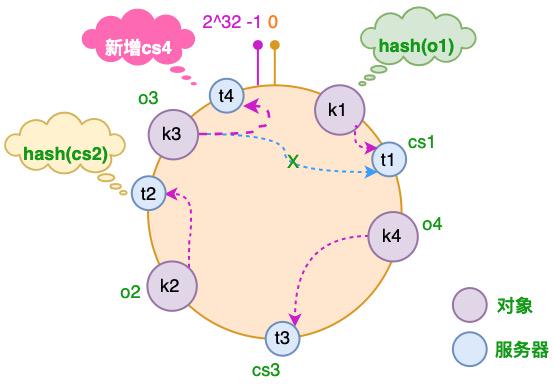
当节点 t4 加入节点时，受影响的只有 t1 节点的元素，重新哈希之后 k3 由 t1 节点转移到 t4 节点，其他节点上的数据不受影响，当 t3 下线的时候，受影响的 t3 节点所有元素将重新哈希到 t2 节点，相比于传统的哈希算法有比较大的提升。

由于节点哈希到哈希环的时候未必是均匀分布的，有可能部分的节点哈希范围很大，部分的哈希范围很小，为此引入虚拟节点来解决负载不均衡的问题。即将每台物理服务器虚拟为一组虚拟服务器，将虚拟服务器放置到哈希环上，如果要确定对象的服务器，需先确定对象的虚拟服务器，再由虚拟服务器确定物理服务器

问答

数组、链表谁快？

遍历数组和链表的时间复杂度是 O(n)，但是在实际中确实数组的速度要比链表快

1. 首先，数组在内存中的地址是连续相邻的，而链表在内存的地址是散列的，不连续的
2. CPU 缓存会把一片连续的内存空间读入， 因为数组结构是连续的内存地址， 所以数组全部或者部分元素被连续存，在 CPU 缓存里面，链表的节点是分散在堆空间里面的，这时候 CPU 缓存帮不上忙，只能是去读取内存，而缓存的速率要比内存快。
3. CPU > 寄存器 > 缓存 > 内存

CUP 取数据，处理数据，都要放到寄存器中处理（存放指令），缓存就是把内存中提取的数据暂时保存在里面。如果寄存器要获取内存中同一位置的数据，就从缓存中获取，如果寄存器获取的不是同一个内存地址的数据（或者获取的内存地址缓存中不存在），就从内存中查找获取

如何判断一棵树是平衡二叉树？

如果某二叉树中任意结点的左右子树的深度相差不超过 1，那么它就是一棵平衡二叉树。